未知のエネルギー散逸系の動的平衡状態を分散した積分器で誘導
- 適応的な同期振動現象の解明に寄与 -
2022/10/27
発表のポイント
概要
同期現象は、多くの自然機械系に共通する現象です。生物の関節の摩擦や減衰は、エネルギー散逸につながります。エネルギー散逸系の動的平衡のためには、1サイクル中の摩擦によるエネルギー損失量とモーターからのシステム全体へのエネルギー入力量が釣り合っている必要があり、力学モデルが未知の機械力学システムや多自由度システムである場合に、どのように環境適応的に動的平衡状態を誘導できるかは自明ではない問題です。
これまでシステムの状態を用いた結合振動子等により振動入力の調整機構を用いる手法が用いられてきました。しかし振動子を用いる場合、振動子の種類の選定が事前に必要となることや、振動子系の力学自体がシステムの振る舞いに大きく影響を与えるという問題がありました。
東北大学大学院工学研究科の林部充宏教授と理化学研究所下田真吾ユニットリーダーの研究グループは、力学モデルの情報がない未知のエネルギー散逸系であっても、その動的平衡の同期振動状態を分散神経積分器により誘導できることを実証しました。
提案の手法ではトルク入力情報を用いた分散積分器のみにより、振動の位相や周波数の情報を用いなくても位相調整、振動数調整、振幅調整現象が自己組織的に起きることで動的平衡状態の誘導をもたらすことを実証しました。自然界にみられる生体の環境適応性のある同期振動現象の解明につながることが期待されます。
本成果は、2022年10月13日に、「Scientific Reports」に掲載されました。
関連動画
Synergetic synchronized oscillation by distributed neural integrators
研究の背景
同期現象は、多くの自然機械系に共通する現象です。人間や動物の関節の摩擦や減衰は、エネルギー散逸につながります。減衰することなくリズムを維持するリミットサイクル注4生成のためには、関節にエネルギーを供給することが必要であり、そのためには、関節に積極的にトルクを加える必要があります。注入エネルギーが散逸エネルギーより小さい場合、システムの運動はいずれ停止します。注入エネルギーが損失エネルギーより大きければ、エネルギーが発散します。明示的なシステムの力学情報が事前に与えられていない未知の環境では、動的平衡をとることは容易ではありません。
従来の方法では、結合振動子を用いて振動子間の入力調整をとることで動的平衡をつくる手法が知られています。位相や振動数の情報を用いて、振動子間の位相差が広がらないようにする方法や、振動子間の振動数を調整する機構などによりフィードバック的な調整により動的平衡をとる方法が知られています。
研究の内容
本研究では未知のエネルギー散逸系において、結合振動子を用いずにリミットサイクルを誘導するシンプルな分散型神経積分器による手法を提案し、その環境適応性を検証しました。その結果、異なる物理環境および多自由度システムにも適応し協調的な同期振動による動的平衡状態を生成できることを実証しました。
まず二重振り子注5の二関節のうち一関節を可動関節にしてリミットサイクルをつくる問題において、リンクの長さを短くし、質量を半分や倍の設定にした環境を与えて事前知識なしに環境適応できるかどうかを検証したところ、リンクの長さの条件の変わった場合だけ、振動の周波数調整を行う挙動を自己組織的に発生できることを示しました。また、実機試験でも検証し外乱を与えてもある一定のリミットサイクルに収束することを確認しました。
二つの二重振り子を共通のベースに固定した場合では、ベースを介した相互作用がある場合には逆相に収束するように自己組織化され、位相調整機能も持つことがわかりました。
最後に多関節が直列につながった環境では、ベースが支持されている環境では関節入力を同相にすることでリミットサイクルを形成し、土台が支持されてない環境では関節入力を逆相にすることでリミットサイクルを形成し、また振動の振幅調整を関節間で行うことで、一番エネルギー損失のない動的平衡振動モードに遷移する挙動が現れることを示しました。
本研究は科学研究費補助金 (新学術領域) 超適応プロジェクト(第一期)20H05458、(第二期)22H04764および(基盤B)18H01399の支援を受けて行われたものです。
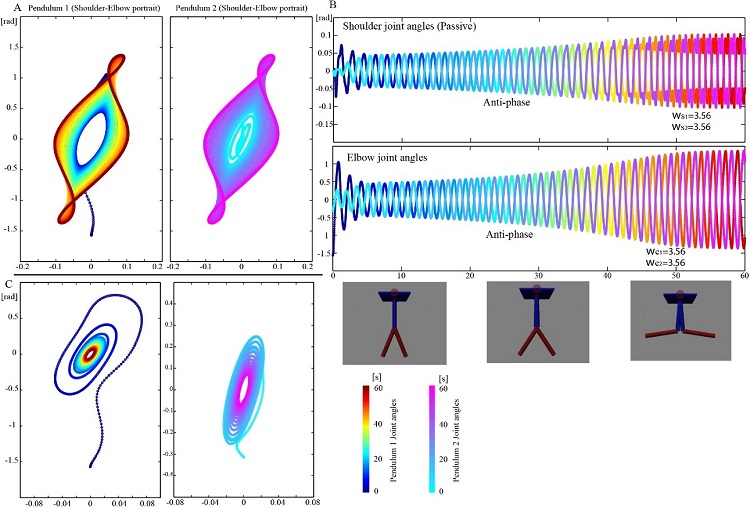
図1 提案した分散神経積分器で制御されたリミットサイクル形成の様子、共通の浮動ベースに接続された二つの二重振り子の位相図。肩関節と肘関節の角度が振り子間で逆位相に調整されながら時間変化し、最終的にシステムの固有周波数に収束する周波数調整も起きている。
研究の意義・今後の展望
本論文の結果は、環境が未知の複雑なダイナミクス問題であっても、単純な分散積分器によって動的平衡振動状態が誘導できることを示したもので、生体が見せる適応的同期振動の誘導がなぜ可能なのかという問題に対して、単純で計算負荷のない原理でも実現できることから、その解明に寄与します。また、本知見は機械力学システムの同期振動現象の解明や動的平衡制御の設計に活用できることを示唆する研究成果であり、更なる応用が期待されます。
用語解説
注1 エネルギー散逸
エネルギーが出入りする開放系では、エントロピーがより低い秩序ある相状態へ系が移行する場合がある。エネルギーの散逸に伴って発生する秩序構造を散逸構造と言う。
注2 結合振動子
微小な振動体を振動という性質にだけ着目したときに「振動子」と呼ぶ。振動現象をしめすもの(振動子)が相互に影響を及ぼしあうようなモデル。例えば隣の振動子の位相がその隣の位相に影響を及ぼすといった局所的な結合もあれば、すべての振動子に同様に影響を与える大域的な結合の様式もある。
注3 環境適応性
環境の変化に応じて行動を切り替える性質や能力を「環境適応性」あるいは「環境適応能力」と言う。
注4 リミットサイクル
力学系における相空間上での閉軌道。安定なリミットサイクルは閉軌道に小さな摂動(運動に攪乱を加える力)が加わっても元に戻る。例えばいつまでも同じリズムで動く時計の振り子や心筋の振動状態をリミットサイクルにあると言う。
注5 二重振り子
振り子の先にもう1つ振り子をつないだもので、カオス理論の説明によく使われる。単独の振り子は規則的な運動をするが、2つをつなぐと両方の動きが合わさって不規則な動きになる。
論文情報
著者: Mitsuhiro Hayashibe, Shingo Shimoda
掲載誌: Scientific Reports, 12, 17163, Oct 2022
DOI: 10.1038/s41598-022-21261-w
URL: https://www.nature.com/articles/s41598-022-21261-w
お問合せ先
東北大学大学院工学研究科 ロボティクス専攻 教授 林部 充宏
TEL:022-795-6970
E-mail:mitsuhiro.hayashibe.e6@tohoku.ac.jp
